黄连金:区块链不可能三角为什么不可突破
摘要
在1985年,由Fischer、Lynch和Patterson三位科学家发表的论文中,提出了FLP理论。FLP理论证明了,在一个完全异步的分布式系统中,如果有一个节点出现故障,没有任何一种共识协议,能够实现完全的一致性。
在2002年,Lynch和Gilbert发表的论文中,提出了CAP理论。CAP理论证明了,在一个分布式系统中,最多只能同时满足一致性(Consistency)、可用性(Availability)和分区容错性(Partition tolerance)这三项中的两项。
区块链作为典型的分布式系统,FLP和CAP同样适用于区块链。本文将基于FLP理论和CAP理论,分析一致性(Consistency)、可用性(Availability)和分区容错性(Partition tolerance)与区块链不可能三角间的逻辑关系,从而解释为什么区块链不可能三角不可突破。
1. FLP理论概要
1985年4月,Fischer,Lynch和Patterson证明的FLP理论,是最重要的分布式系统理论之一,他们也凭借论证FLP理论的论文,获得了分布式计算中最具影响力的Dijkstra论文奖。
FLP理论证明了,在异步通信系统中,存在节点失效(即便只有一个),不存在一个可以解决一致性问题的确定性算法。
在同步的系统中,达成共识是可以被解决的。因为在同步系统中,当有进程出现故障,或者响应超时,我们可以认定它已经崩溃。
在异步的系统中,当一个进程出现故障,或者响应丢失时,是无法检测到的。在这样的条件下,如果其中有任意一个进程出现问题,没有任何一个分布式算法,可以让所有的非故障进程,达成一致性共识。
因为有FLP不可能性的限制,大部分区块链项目的共识算法都把大部分节点是诚实的 满足和一定的同步性作为前提。POW认为51% 的节点是诚实的,并且有一定的同步性。POS和PBFT也认为大部分节点(66%)是诚实的.
2. CAP理论概要
在2000年的分布式计算原则研讨会(PODC)上,计算机科学家埃里克.布鲁尔针对分布式计算系统的一致性(Consistency)、可用性(Availability)、分区容错性(Partition-tolerant)提出了猜想。在2002年,他的猜想得到了来自麻省理工学院的两位教授Nancy Lynch 和 Seth Gilbert的证明,并被称为CAP定理。
CAP定理证明了:当网络存在分区时,提供可靠的原子一致性数据是不可能的,但是想要实现一致性、可用性、分区容错性,三个属性中的两个是可行的。在异步通信系统中,当没有锁提供时,如果出现消息丢失,即使允许过时的数据返回,提供一致性数据也是不可能的。在同步通信系统中,可以在一致性和可用性间取得一定的平衡。
2.1. 一致性(Consistency)
CAP理论的论证中,把一致性定义限定在原子数据对象上,这和其他大多数正式定义一致性服务的方法相同。满足一致性条件的系统,对所有操作都有统一记录,这些操作记录看起来像是一个单独的实例完成的。这要求分布式系统的所有请求必须进行同步,然后才能执行操作。最终呈现的结果,像是同一个节点在同一时间响应,然后执行的一样。
这是提供给用户理解的,最简单的一致性保障模型,也是给设计分布式客户端应用的人理解的最简单的模型。
2.2. 可用性(Availability)
为了能让分布式系统持续可用,每个请求会被发送给一个系统中的正常节点,并收到响应。这是任何分布式服务使用的算法必须要满足的。
CAP理论的论证中,将可用性定义为两种:
l 弱可用性:在终止之前,算法运行的多久是没有边界的,因此允许没有边界的计算。
l 强可用性:当服务网络发生错误时,每个请求也必须被响应。
在弱可用性条件下,系统对响应时间可以不做保证,但是必须做出响应,当系统出现错误时,并不保证对请求做出响应。而在强可用性条件下,即使系统出现错误,请求也必须得到响应。
2.3. 分区容错性(Partition-tolerant)
CAP理论的论证中,分区指的是,网络中允许丢失从一个节点发送到另一个节点的任意数量的消息。这意味着当网络中出现分区时,从一个分区中的节点发送给另外一个分区的节点的消息将会全部丢失。
分区容错指的是,在出现分区时,系统依然能够满足以上定义中的一致性和可用性。原子性要求意味着每一个响应将会是原子性的,尽管任意作为算法的一部分的消息可能不会被传递。可用性要求意味着,每个节点收到的客户端请求必须被响应,尽管任意的消息都可能丢失。
3. 用CAP理论来解锁区块链不可能三角为什么不可突破
在区块链领域中,安全性、可扩展性、去中心化,三者被称作区块链的“不可能三角”,意思是说,在同一个区块链系统中,想要同时做到三者,并且都达到足够高的要求,是不可能做到的。
我们的基本论证思路是,CAP理论在分布式系统中成立,区块链属于分布式系统,区块链必然遵守CAP理论,只要能证明CAP理论中的一致性(Consistency)、可用性(Availability)和分区容错性(Partition tolerance),与区块链的不可能三角存在相应的逻辑关系,即可证明区块链不可能三角不可突破。
3.1. 一致性与安全性
在CAP理论的证明过程中,证明了在异步网络模型中,实现一个读/写数据对象同时具备可用性和一致性是不可能的。我们将该结论和证明过程,对应到区块链系统中。
在CAP理论限定的网络环境中,我们假设一个区块链系统中,存在A和B两个节点,其中A和B同时记录了一个地址H的加密货币余额为X1,此时A和B出现了分区。
当用户在A节点所在的分区发起一笔交易时,地址H中的余额将会发生变化,成为X2。当用户在B节点所在的分区发起一次余额查询操作时,地址H中的余额依然是X1。由此我们说区块链系统中,出现了账本不一致的情况。
当区块链系统中出现不一致状态时,我们认定这样的区块链系统是不安全的。在这样的定义下,一致性是区块链系统安全的基本前提。或者说区块链的安全性是比分布式系统的一致性更加严格的需求。安全性>一致性。
3.2. 可用性与可扩展性
在CAP理论的可用性定义中,分为弱可用性和强可用性,但是这两种可用性都要求,系统可以对所有正常请求做出响应。从技术的角度来讲,即是可以实现正常的可读可写。
在区块链系统中,可扩展性指的是,每秒可以处理的交易量。从技术的角度来讲,高可扩展性即是实现每秒钟高频次的可读可写操作。
从逻辑上,我们可以看出,可用性是比可扩展性更基础的网络要求,不能实现可用性的区块链系统,是不能实现可扩展性的,即是可用性是可扩展性的前提。或者说区块链的可扩展性是比分布式系统的可用性更加严格。可扩展性>可用性。
3.3. 分区容错性与去中心化
在CAP理论中,分区被认为是分布式系统必然存在的。事实也的确如此,在真实分布式环境中,不可能保证系统中的每个节点,都不会出现任何故障。
去中心化作为区块链的基本特征,意味着区块链系统必然是分布式的,也就是说去中心化必定导致发生分区的可能,由此也意味着分区容错性是实现去中心化的前提。
3.4. 现有共识算法对CAP的平衡
在CAP理论中,分区被认为是分布式系统必然存在的,所以讨论没有分区情况的分布式系统是没有意义的。区块链作为典型的分布式系统,其不同的共识算法在满足分区的前提下,对系统的一致性(Consistency)和可用性(Availability)做出了一定的平衡。
Tendermint: Tendermint是POS类型的共识算法,主要包括NewHeight -> Propose -> Prevote -> Precommit -> Commit五个阶段。其中Propose -> Prevote -> Precommit属于共识阶段,是算法的核心,被称作一个Round。在进行区块的提交确认时,一个区块可能需要多个Round。在多个Round中,区块的高度并不会增加,只是向系统提交空块,并且一个区块一旦被确认,是不可能被修改的。所以Tendermint理论上有可能被卡住,区块高度永远不会增加。 这意味着Tendermint在出现分区时,更加侧重于一致性(Consistency)。
Casper FFG: Casper FFG是POS类型的共识算法。在Casper FFG的设计中, 优先考虑一致性,因为它不允许在没有绝大多数验证者同意的情况下完成checkpoint,这样区块也就不会达到最终的确认状态。
Algorand: Algorand是POS类型的共识算法。Algorand与Tendermint的设计中有类似的地方,当出现一致性和可用性冲突时,系统会更倾向于产生空块,不会产生真正意义的区块。所以Algorand更优先考虑一致性。
Dfinity: Dfinity是POS类型的共识算法。当网络出现分区时,它会自动使随机信标暂停,不允许网络中的任何分区继续。所以Dfinity更优先考虑一致性。
POW:当使用POW的网络出现分区时,所有的分区都可以正常的进行出块,等到网络恢复,分区结束时,会遵循最长链原则,不同分区的链将会进行合并,最终成为一条链。因此POW优先考虑可用性。
POC:POC的全称是Proof of Credit ,是全球开源社区项目NULS,创新使用的共识算法。当使用POC的网络出现分区时,所有分区都可以正常进行出块。等到网络恢复时,这里和POW不同的是,如果在POC算法限定的时间内,将会遵循最长链原则,进行区块链的合并;如果超过限定的时间,系统将认为已达到不可逆状态,将不会进行合并。因此POC优先考虑的是可用性。
|
共识算法 |
A(Availability)和C(Consistency)的比较 |
相关项目 |
|
Tendermint |
A<C |
Cosmos |
|
Casper FFG |
A<C |
ETH |
|
Algorand |
A<C |
Algorand |
|
Dfinity |
A<C |
Dfinity |
|
POW |
C<A |
BTC |
|
POC |
C<A |
NULS |
注:A<C代表该共识算法更优先考虑Consistency;
C<A代表该共识算法更优先考虑Availability;
4. 结论
通过以上对一致性(Consistency)与安全性、可用性(Availability)与可扩展性、分区容错性(Partition-tolerant)与去中心化的逻辑关系推导,我们可以得出以下结论:
l 一致性(Consistency)是安全性的必要条件
l 可用性(Availability)是可扩展性的必要条件
l 分区容错性是去中心化的必要条件
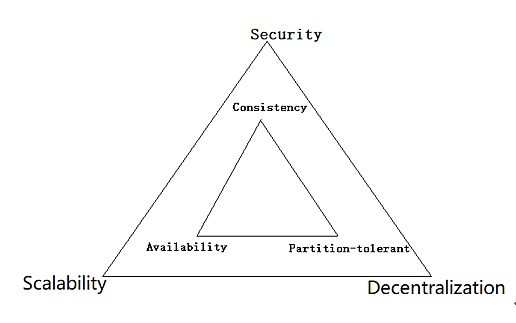
又通过CAP理论可以知道一致性、可用性、分区容错性是不能同时满足的,所以我们可以得出:在CAP理论限定的条件下,安全性、可扩展性、去中心化不能同时满足,即是区块链的不可能三角不可突破。
作者简介:
黄连金
著名区块链专家,核聚链首席科学家、美国 DistributedApps CEO、中国电子学会区块链分会专家委员、NULS技术顾问。
向文波
Java软件工程师,Cryptotech-Writer,NULS Core Team成员。专注于区块链技术研究和区块链解决方案。
参考文献:
Brewer's conjecture and the feasibility of consistent, available, partition-tolerant web services Seth Gilbert,Nancy Lynch
Impossibility of Distributed Consensus with One Faulty Process MICHAEL J. FISCHER,NANCY A. LYNCH,MICHAEL S. PATERSON
分布式系统的CAP理论:https://www.hollischuang.com/archives/666
比较各种共识算法的Finality和Liveness:
https://www.odaily.com/post/5134107
Finality in Blockchain Consensus:
https://medium.com/mechanism-labs/finality-in-blockchain-consensus-d1f83c120a9a

 浪花财经
浪花财经