技术派丨Casper与V神的博弈论

众所周知，Casper 是以太坊从 PoW 转型到 PoS 的一个优化版 PoS 共识机制，以太坊创始人 V 神有意通过 Casper 来硬分叉以太坊以实现这个转型。Casper 是一种以博弈论为基础的共识机制。

为什么这么说？区块链与博弈论有什么关系？不妨往下看！

是什么博弈论？

博弈论是一个分析工具包，它被设计用来帮助我们理解所观察到的决策主体相互作用时的现象。这种理论隐含的基本假设是：决策主体追求确定的外部目标（他们是理性的）并且考虑他们自身的知识或其他决策主体行为的期望（他们推理具有战略性）。

博弈论思想历史久远，比如中国古代的《孙子兵法》。早年的博弈论最初主要研究象棋、桥牌、赌博中的胜负问题，人们对博弈局势的把握只停留在经验上, 没有向理论化发展，正式发展成一门学科则是在20世纪初。

对于博弈论的研究，开始于策墨洛(Zermelo)、波雷尔(Borel)及冯·诺伊曼(VonNeumann)，后来由冯·诺伊曼和奥斯卡·摩根斯坦(Oscar Morgenstern)首次对其系统化和形式化。随后约翰·福布斯·纳什(John Forbes Nash Jr.)利用不动点定理证明了均衡点的存在，为博弈论的一般化奠定了坚实的基础。

在经济学的角度来看，大家认为现代经济博弈论是在20世纪50年代由美国著名数学家冯·诺依曼和经济学家奥斯卡·摩根斯坦引入，目前已成为经济分析的主要工具之一，对产业组织理论、委托代理理论、信息经济学等经济理论的发展做出了非常重要的贡献。1994年和 1996年的诺贝尔经济学奖分别颁发给了做博弈论方向研究的经济学家。

博弈论考虑的是一个有特定规则的群体环境的个体的预测行为和实际行为，最基本的要素有三个：参与者(Player)、策略(Strategy)和收益(Payoff)。博弈论假设：

1、参与者是理性的，最大化自己的利益；

2、参与者对所处环境及其他参与者的行为形成正确信念与预期。

也就是说在一策略组合中，所有的参与者会遇到这样一种情况：当其他人不改变策略时，他此时的策略是最好的，这也就是著名的纳什均衡（Nash Equilibrium）。在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动，此时如果他改变策略，他的利益将会降低。

根据不同的基准博弈有不同的分类。一般认为，博弈主要可以分为合作博弈和非合作博弈。二者的区别在于，相互发生作用的当事人之间有没有一个具有约束力的协议，如果有就是合作博弈，如果没有就是非合作博弈。

从行为的时间序列性，博弈论进一步分为静态博弈、动态博弈两类：静态博弈是指在博弈中参与人同时选择，或虽非同时选择但后行动者并不知道先行动者采取了什么具体行动；动态博弈是指在博弈中参与人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。对这种分类通俗的理解："囚徒困境"就是同时决策的，属于静态博弈；而棋牌类游戏等决策或行动有先后次序的，属于动态博弈。

按照参与者对其他参与者的了解程度，分为完全信息博弈和不完全信息博弈。完全博弈是指，在博弈过程中每一位参与者对其他参与者的特征、策略空间及收益函数有准确的信息；不完全信息博弈是指，参与者对其他参与者的特征、策略空间及收益函数信息了解得不够准确、或者不是对所有参与者的特征、策略空间及收益函数都有准确的信息。

纳什均衡

我们再回到经典的囚徒困境（Prisoner's Dilemma）问题来阐释博弈论与加密经济学相关的核心——纳什均衡：

假设有两个参与者和一个庄家，每个参与者有一式两张卡片，各印有“合作”和“背叛”。两个参与者各把一张卡片文字面朝下，放在庄家面前。文字面朝下排除了参与者知道对方选择的可能性。然后，庄家翻开两个参与者卡片，根据以下规则支付双方收益：

• 一人背叛、一人合作：背叛者得5分（利益驱动），合作者0分（受骗支付）。

• 二人都合作：各得3分（合作报酬）。

• 二人都背叛：各得1分（背叛惩罚）。

决策收益矩阵如下：

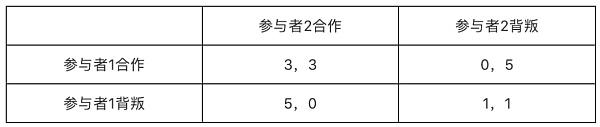
我们可以看到这种情况下的纳什均衡是参与者1和2都合作，合作在团体而言是支配性策略。

但这里面有个问题，如果在一个像区块链这样没有信任基础的环境（比如分叉的收益大于在原来链上挖矿的收益）下，参与者1和2都背叛的收益大于都合作怎么办？这样的一个决策收益矩阵如下:

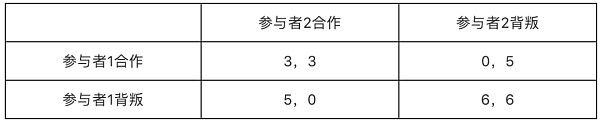
因为在区块链上很可能出现参与者为了个人的利益最大化而完全不顾及整体利益的情况，这时候“惩罚”机制就显得尤为重要了。如果我们能设置一个机制即每一个背叛（对整体利益不利）的行动我们都额外惩罚6分，新的决策收益矩阵就变成了这样：

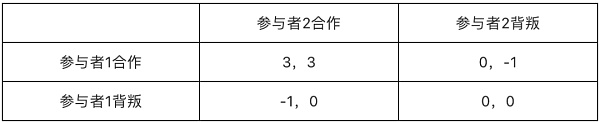
我们可以看到当加入了惩罚机制之后，纳什均衡从参与者都背叛（作恶）变成了都合作。这个机制在区块链的经济模型当中是非常重要的一个环节。 

谢林点

谢林点（Schelling point，又译为薛林点或聚焦点），是博弈论中人们在没有沟通的情况下的选择倾向，做出这一选择可能因为它看起来自然、特别，或者与选择者有关。这一概念是由美国诺贝尔奖获得者托马斯·谢林（Thomas Schelling）于1960年在《冲突的策略》一书中提出的。在该书中（57页），谢林描述：“每个人期望的聚焦点是，他人期望他本人期望被期望做出的选择。”这种概念后来以谢林的名字命名。

比如一群独立不交流的人，被要求从以下数字当中选出一个数字，且只有大家都选的是同一个数字时才能获得奖励：

• 38219057301490231

• 100000000000

• 1.43123289

大家可能都会同时选择100000000000这个数字，因为它看起来最自然，同时也是大家最预期其他人会选的数字，其他两个数字并没有什么显著的特点。

有限理性模型

另一个对加密经济学很关键的博弈论概念是“有限理性模型”(Bounded Rationality Model)。20世纪50年代之后，人们认识到建立在完全理性决策理论之上的经济体只是一种理想模式，不可能指导实际中的决策。赫伯特·西蒙（Herbent Simon）提出了满意标准和有限理性标准，用“社会人”取代“经济人”。 有限理性模型又称西蒙模型或西蒙最满意模型，是一个比较现实的模型，它认为人的理性是处于完全理性和完全非理性之间的一种有限理性。

有限理性模型认为决策者追求理性，但又不是最大限度地追求理性，他只要求有限理性。这是因为人的知识、能力或者时间等有限，决策者既不可能掌握全部信息，也无法认识决策的详尽规律。同时，有限理性模型认为决策者在决策中追求“满意”标准，而非最优标准。

我们举个例子，小李每天都有习惯健身房打卡健身，突然有一天打卡的时候发现前台没有人，同时桌子上有5块钱，有限理性模型认为这时候小李不会去拿这5块钱，因为选择不拿是小李最习惯、最简单的决策，如果拿了5块钱或许以后对小李每天来健身的影响更大，所以小李会在有限的条件下做出不拿这5块钱的决定。这个概念对于加密经济学中作恶部分机制的设计有着重要的启发作用。

博弈论机制设计与共识机制

区块链上共识机制的设计与博弈论机制设计最为相似，机制设计通常被称作反向博弈论，因为我们是从一个期望的结果开始，反向推导来设计一个完整的游戏。如果在游戏中玩家会追求自身的利益，那就会产生我们想要的结果。例如，想象一下我们负责设计一个拍卖规则，我们的目标是希望投标人能够以一个产品的实际价值中标。为了达到这个目的，我们运用博弈论理论将拍卖设计成一种游戏，其中每个玩家的核心策略都是能够以真实价值竞拍。

和博弈论机制设计一样，共识机制设计着重于系统的设计和体系的建立。就像在拍卖例子中，我们用博弈论来设计一套能够产生一定制衡结果的规则或机制，在共识机制设计中，我们使用密码学和计算机编程来实现这种经济激励机制，我们设计的系统通常都是分布式与去中心化的。

比特币的共识算法PoW正是这种方法的产物。中本聪希望比特币具备某些特性，比如它能够就其内部状态达成共识，并且具备抗审查的能力。然后，他在假设人们以合理的方式回应经济激励的基础上，设计了整个比特币系统来实现这些特性。

博弈论机制设计与区块链安全

现实商业世界当中，恶意收购是一个非常影响公司安全的行为，恶意收购者通常不经过对方同意，并希望取得控制性和对方已有的一切资源。区块链的世界当中，也有类似的安全隐患存在，就是贿赂攻击者模型(Bribing Attacker Model)。

贿赂攻击者模型指的是在一个非协作选择模型(UncoordinatedChoice Model)如无信任基础的区块链(Trustless Blockchain)上，存在一个拥有足够资源的贿赂者，通过额外的经济奖励（贿赂）来激励其他参与者采取特定行动的攻击行为。这里的特定行动通常对原有区块链体系的安全有较大影响，最常见的是恶意分叉。

如果我们用恶意收购来类比贿赂攻击者模型，可以这样阐释：一个区块链协议之外的贿赂者，通过一个条件来收购代币或者挖矿算力，从而达到攻击原有区块链的目的。通俗地讲，叫做“收买现有节点”。

为了更好地理解贿赂者是如何实现其目的，我们用通俗的博弈论知识来做分解。

假想一个简单的投票机制，区块链上每个参与者都可以投0和1两个决策，假设0这个决策是对原来区块链有利的，1是对原来区块链不利的，机制规定只有大家投的结果一样大家才能获得相应的奖励P，这种情况下的纳什均衡是大家都投0，即对原来区块链有利的决策，用决策收益矩阵表示如下:

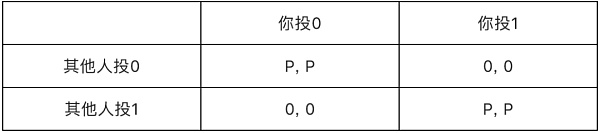
如果这个时候出现了一个贿赂攻击者，他告诉你如果你投1同时其他人不投1的话，除了能得到奖励P以外，还有额外的报酬 ε，那么新的决策收益矩阵就如下所示：

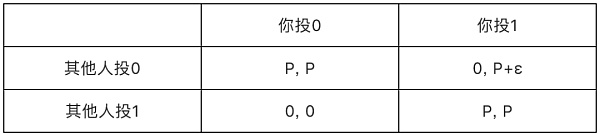
表面上来看，对于你来说投1是最好的选择。可问题是，当贿赂者告诉所有人这个贿赂条件的时候，所有人都会觉得投1是最好的选择，那么这个时候的纳什均衡就变成了大家都投1，即大家都选择了对原来区块链不利的决策。

贿赂者通过这个P+ε攻击实现了他的目的，同时还不用真正去支付他承诺的贿赂金ε，就成功地使大家都做出了对原来区块链不利的决策。很聪明、很巧，是不是？这个P+ε攻击问题也是类似于PoW共识机制的其中一个安全隐患。

其中一个解决办法是引入有保证金和惩罚措施的改进版PoS共识机制。由于每个区块链的参与者都有保证金押在链上，如果贿赂者让你去做出对原来区块链不利的决策，你就会损失你所有的保证金，你会觉得这样做得不偿失。更何况从上述的决策收益矩阵当中我们还知道，就算你做出了对原来区块链不利的决策，也拿不到贿赂者承诺的额外报酬ε。

以博弈论为基础的共识机制前瞻——以太坊Casper共识算法

Casper是以太坊从PoW转型到PoS的一个优化版PoS共识机制，以太坊的核心贡献者V神有意通过Casper来硬分叉以太坊以实现这个转型。

总的来说，Casper要求验证人（validator）用保证金中的大部分对共识结果进行下注。而共识结果又通过验证人的下注情况形成：验证人必须猜测其他人会赌哪个块胜出，同时也下注这个块。如果赌对了，他们就可以拿回保证金外加交易费用，也许还会有一些新发的货币；如果下注没有迅速达成一致，他们只能拿回部分保证金。因此数个回合之后，验证人的下注分布就会收敛。

此外，如果验证人过于显著地改变下注，比如先是赌某个块有很高概率胜出，然后又改赌另外一个块有高概率胜出，他将被严惩。这条规则确保了验证人只有在非常确信其他人也认为某个块有高概率胜出时才以高概率下注。只要验证人足够多，Casper就可以通过这个机制来确保不会出现下注先收敛于一个结果然后又收敛到另外一个结果的情况。验证人对每一个高度h上的每一个候选块独立下注，给每个块指定一个胜出概率并公布。

通过反复下注，对于每个高度h，验证人会选出唯一的一个胜出块，这个过程也决定了交易执行的顺序。如果一个验证人在某个高度公布的概率分布总和大于100%，或者公布了小于0%的概率，或者对一个无效块指定了大于0%的概率，Casper将罚没他的保证金。

简而言之，Casper权益证明尝试提供一个非常巨大的加密经济学安全边际，通过强制要求大笔的以太坊安全保证金代替计算机算力，以实现验证者的功能。这一安全保证金或者说加密经济学证明，成了一个强有力的威慑。其含义是一目了然的——在区块链上制造麻烦，你就将失去一切。

Casper强制参与者加入一个谢林币（Schelling Coin）游戏。参与者们被强制要求将他们的安全保证金押在多数人将下注的事情上。使用同样的递归逻辑，多数参与者将准确地投票给有效的交易，因为每个参与者都预期其他人得出同样的结论。情形就是如此，权益证明可以抵抗P+ε攻击，因为在他们最终将投票给少数方的情形中，攻击者将不得不提供非常巨额的预算以补贴参与者的安全保证金。

在这些安全模型的环境下，我们可以看出Casper的弹性集中在不协调选择模型中，且源自贿赂攻击者。Casper在理论上同样对起源于合作攻击者模型的51%攻击敏感。但是，就像比特币一样，以太坊将做出如此攻击的成本提高到如此高昂的地步，以至于几乎完全遏制了它。在Casper的环境下，失去所有相关权益的威胁是一个更强有力的震慑。